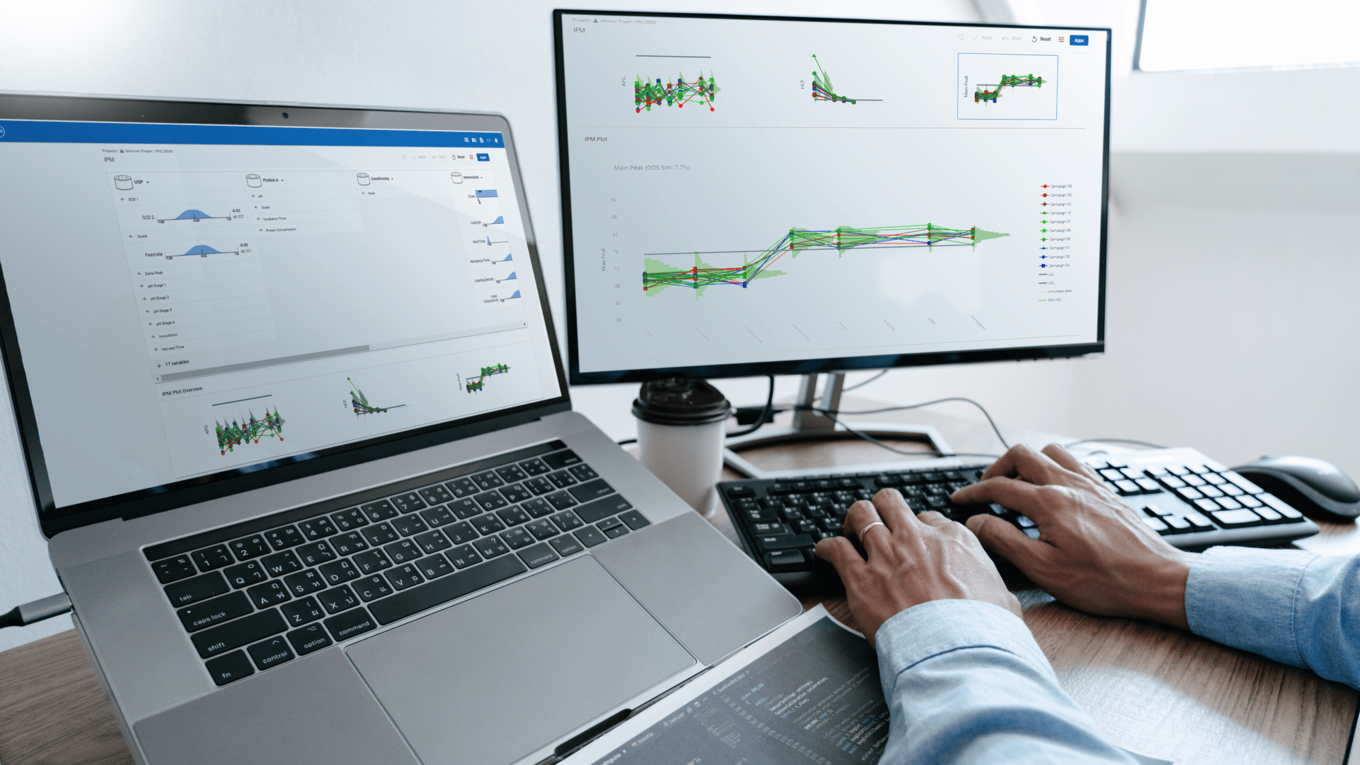
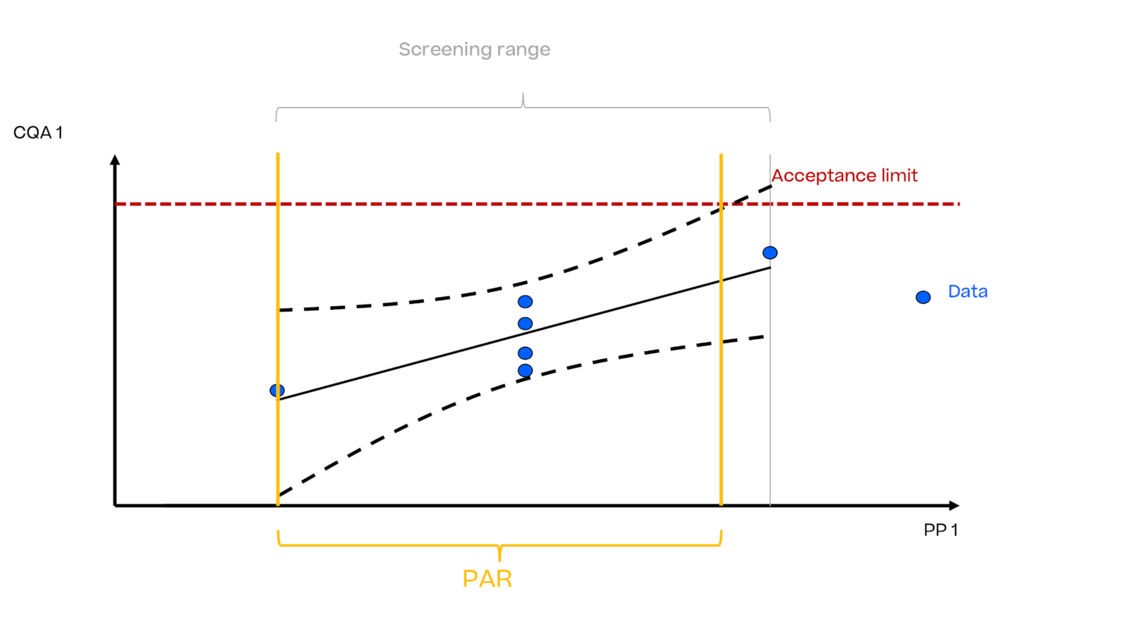
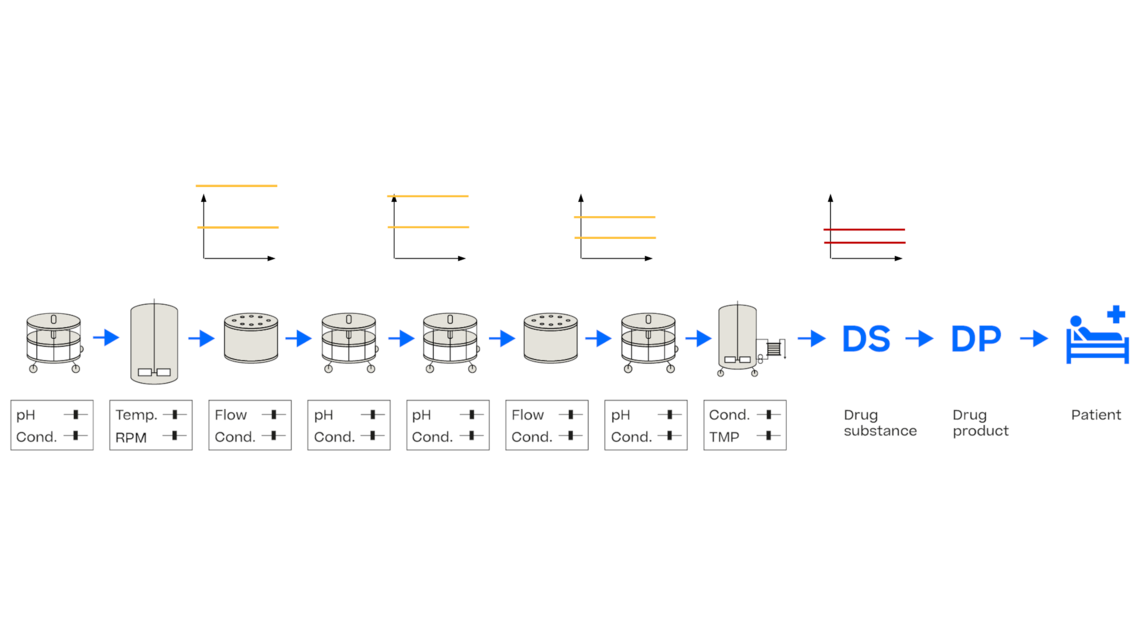
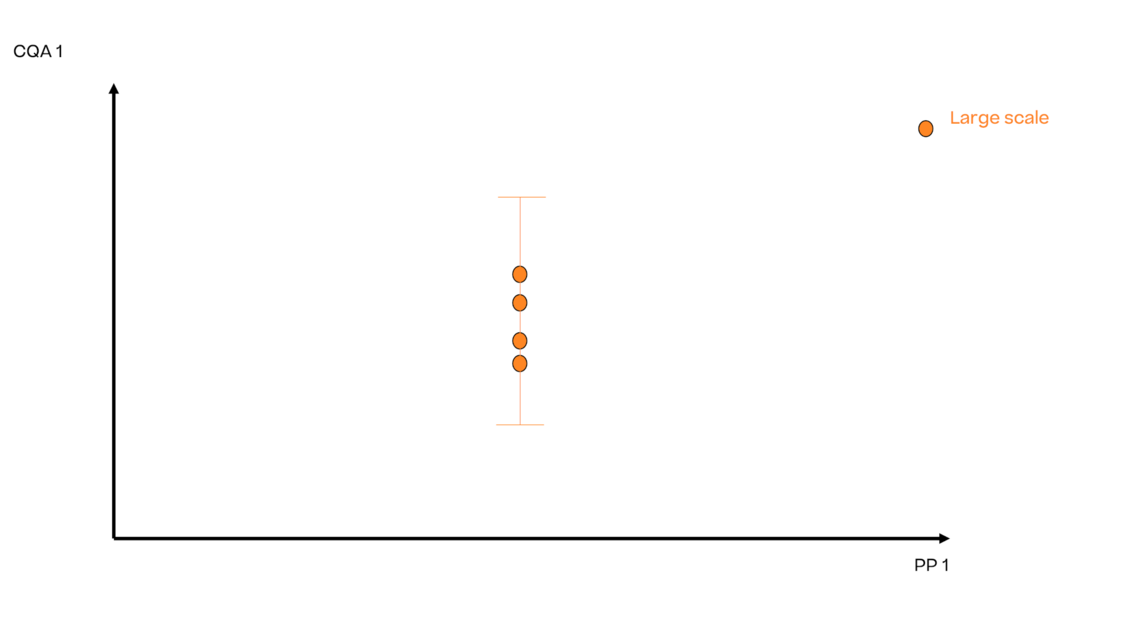
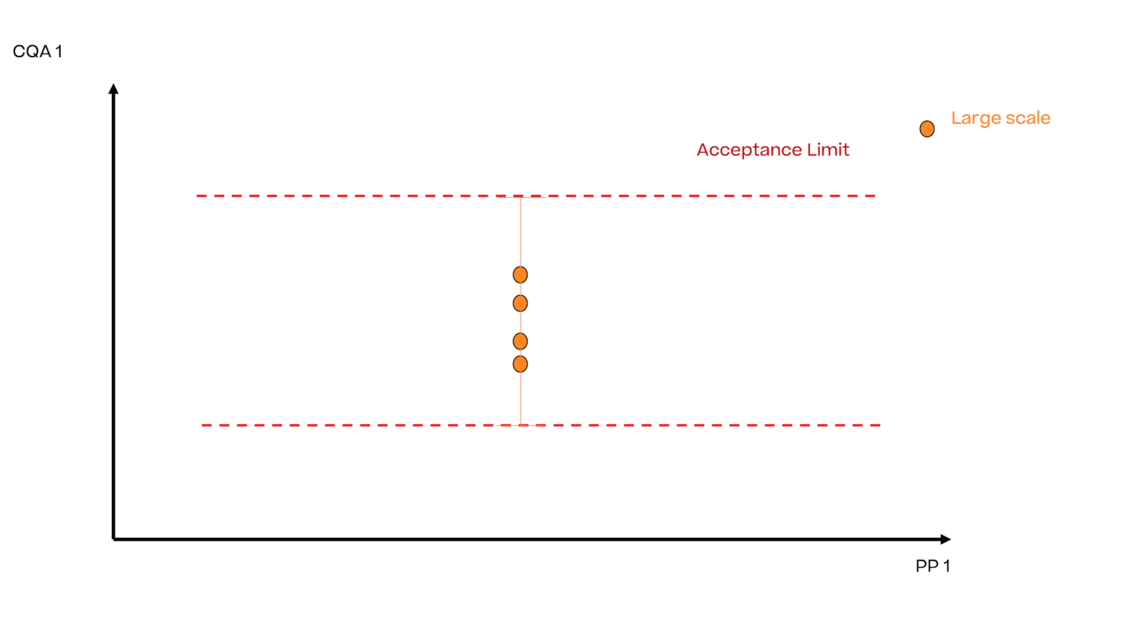
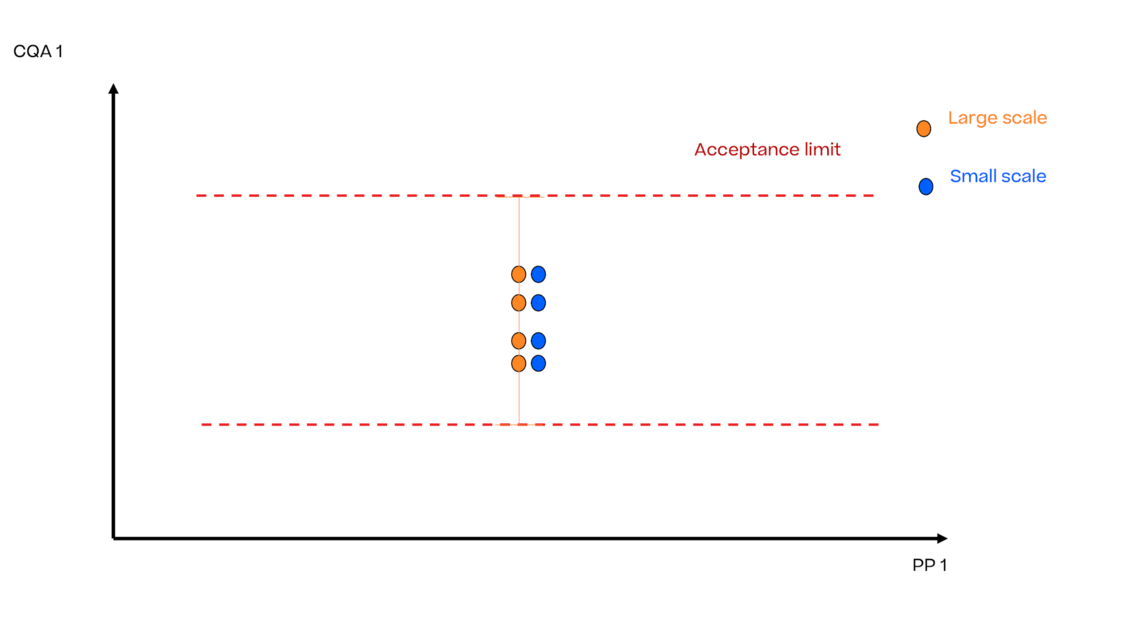
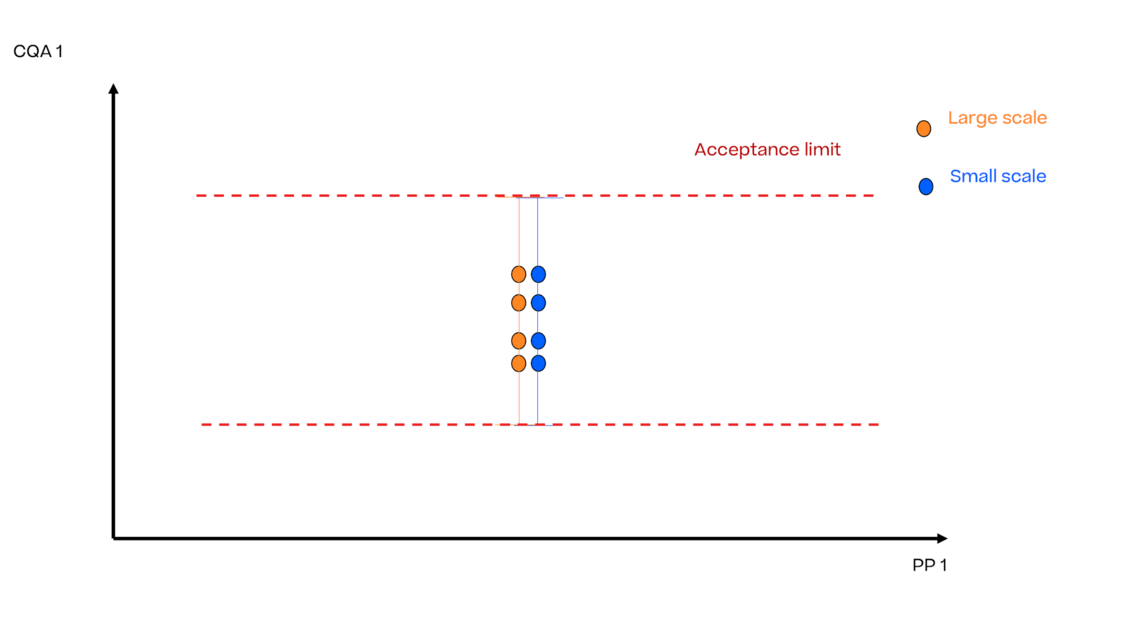
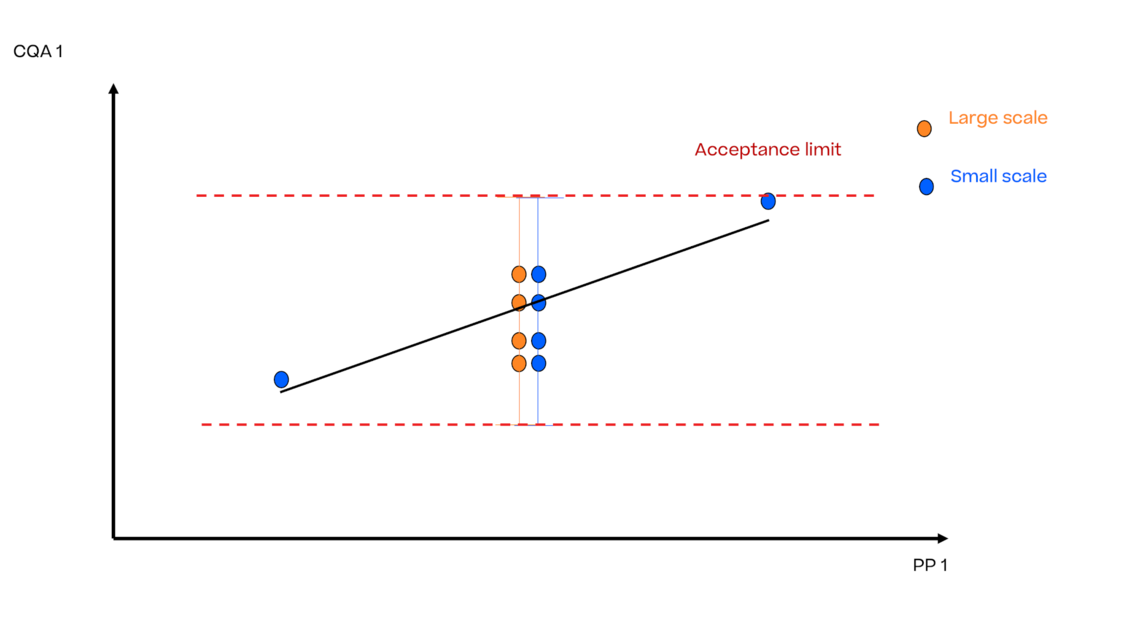
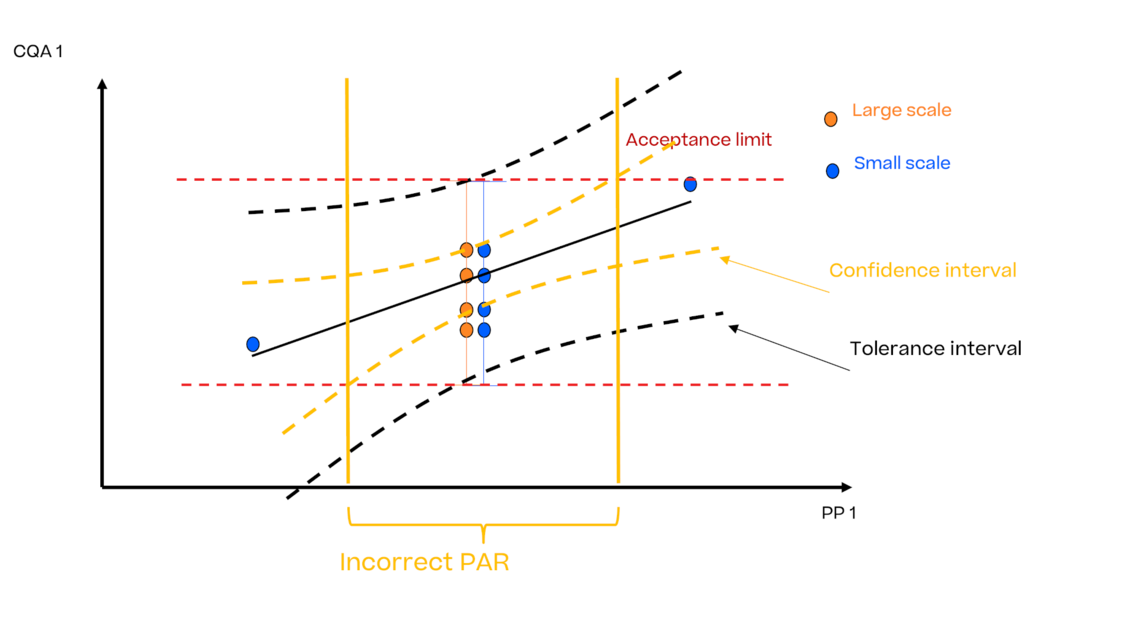
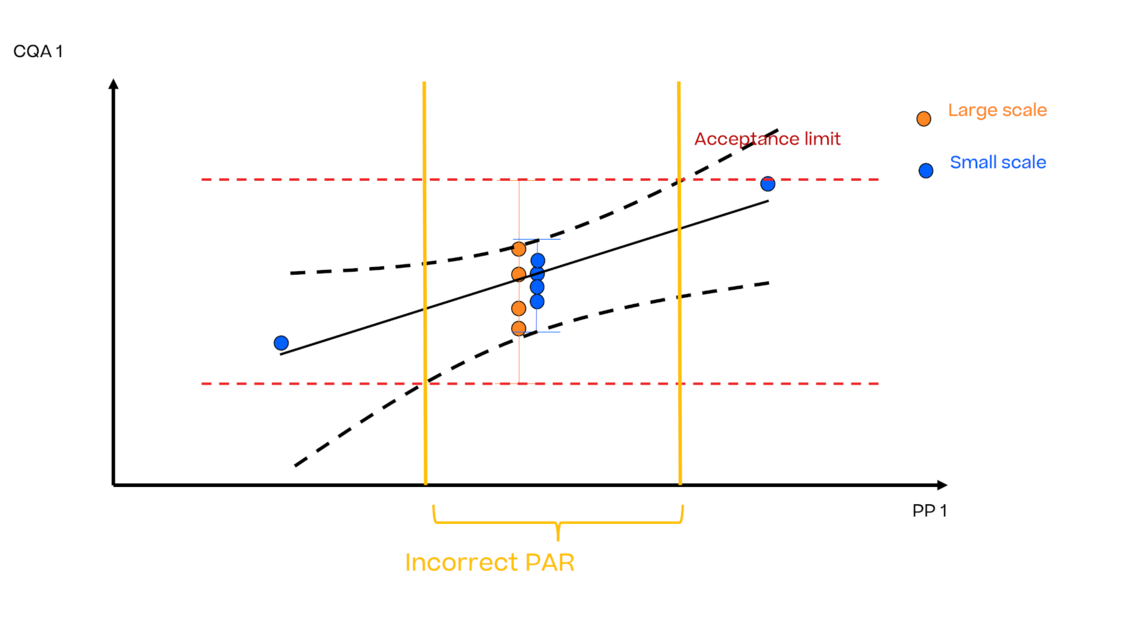
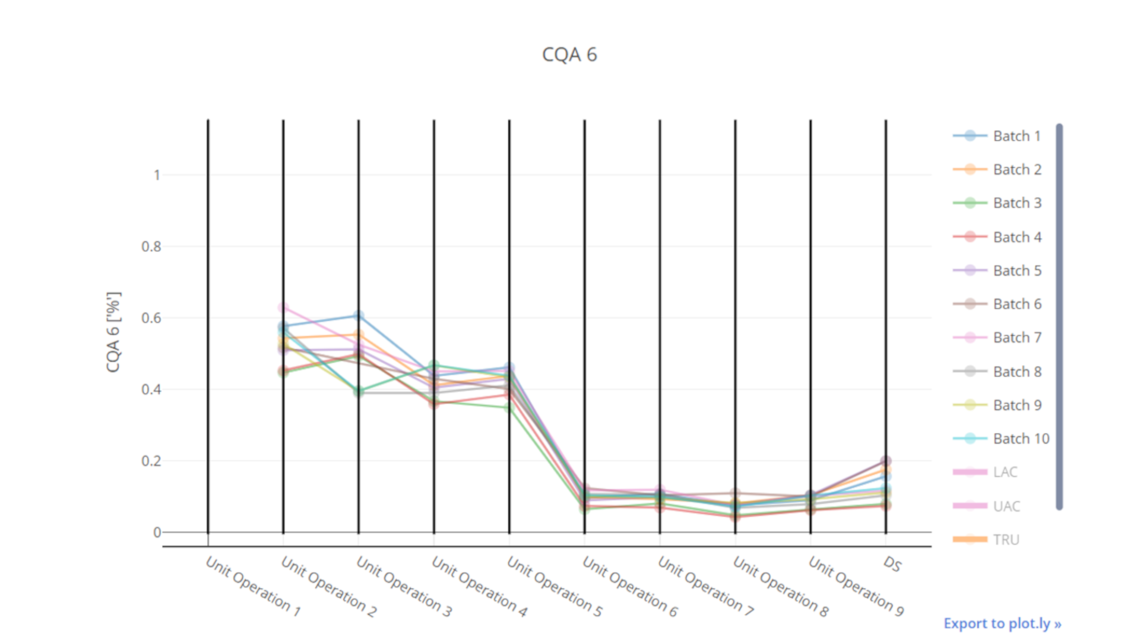
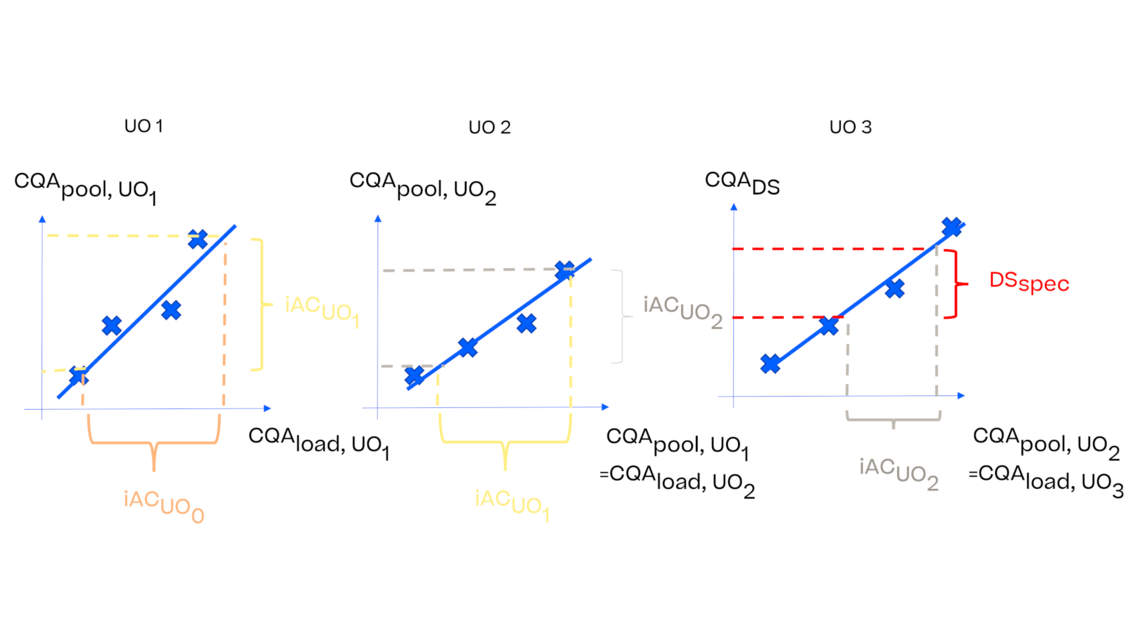
In this article we want to demonstrate one of the biggest flaws in setting control strategies in biopharmaceutical manufacturing. This is linked to the fact that people still set specifications, either drug substance specification, or intermediate acceptance criteria/ in process controls, based on a x-SD approach. Moreover, we want to demonstrate sound tools that enable a data driven establishment of those limits and herein derived control strategies (Marschall et al., 2022).
This article mainly focuses on examples from biopharmaceutical manufacturing but can be applied without loss of generality to other pharmaceutical and chemical processes.